Iracionální číslo je a reálné číslo které nelze vyjádřit jako jednoduchý zlomek nebo podíl dvou celých čísel. Na rozdíl od racionálních čísel, která lze zapsat jako zlomky, iracionální čísla mají desítkové zastoupenís které ani nekončí, ani se neopakují. Příklady iracionálních čísel zahrnují √2, π (pi) a e (Eulerovo číslo). Tato čísla mají nekonečné neopakující se desetinné rozšířenís a nelze je vyjádřit zlomkem. Iracionální čísla mají jedinečné vlastnosti a hru Významnou roli v matematice a různé vědecké obory.
Key Takeaways
| Iracionální číslo | Definice |
|---|---|
| √ 2 | Druhá odmocnina ze 2, což je přibližně 1.41421356 |
| π (pí) | Poměr obvodu kruhu k jeho průměru, přibližně 3.14159265 |
| e (Eulerovo číslo) | Matematická konstanta, která je přibližně 2.71828183 |
Pochopení iracionálních čísel
Iracionální čísla jsou v matematice fascinujícím pojmem. Oni jsou typ of reálné číslo které nelze vyjádřit jako zlomek nebo podíl dvou celých čísel. Na rozdíl od racionálních čísel, která lze zapsat jako koncová nebo opakující se desetinná místa, iracionální čísla mají nekonečný desetinné rozšířenís které ani nekončí, ani se neopakují.
Jednoduchá definice iracionálních čísel
Zjednodušeně řečeno, iracionální čísla jsou čísla, která nelze vyjádřit jako zlomek nebo podíl. Nejsou-opakující se a neukončující desetinná místa. Tato čísla často vznikají, když bereme náměstí kořen nedokonalý čtverec, Jako náměstí kořen 2 nebo náměstí kořen 5. Projekt desítkové zastoupení of tato čísla pokračuje navždy bez jakéhokoli vzoru.
Symbol označující iracionální čísla
V matematice se iracionální čísla běžně označují symbol „π“ (pí). Pi je matematická konstanta což představuje poměr obvodu kruhu k jeho průměru. Je to iracionální číslo s nekonečnem desetinné rozšíření která se nikdy neopakuje. Pi se přibližně rovná 3.14159, ale jeho desítkové zastoupení pokračuje navždy bez jakýkoli rozpoznatelný vzor.
Příklady iracionálních čísel
Existují četné příklady iracionálních čísel, která přitahovala matematiky v celé historii. Tady jsou několik známých příkladů:
Druhá odmocnina z 2 (√2): Toto je jedna z nejznámější iracionální čísla. Nelze jej vyjádřit jako zlomek nebo podíl a má nekonečno desetinné rozšíření že se to neopakuje. Přibližná hodnota √2 je 1.41421356.
Pi (π): Jak již bylo zmíněno dříve, pí je iracionální číslo, které představuje poměr obvodu kruhu k jeho průměru. Své desítkové zastoupení pokračuje navždy bez opakování. Přibližná hodnota pí je 3.14159.
Zlatý řez (φ): Zlatý řez je iracionální číslo, které po staletí fascinuje matematiky, umělce a architekty. Přibližně se rovná 1.6180339887 a často se vyskytuje v přírodě a umění.
Eulerovo číslo (e): Eulerovo číslo je další důležité iracionální číslo v matematice. Přibližně se rovná 2.71828 a objevuje se v různé matematické a vědecké souvislosti, jako je exponenciální růst a složený úrok.
Tyto příklady ilustrovat rozmanitá příroda iracionálních čísel a jejich přítomnost in různé větve matematiky. Hrají zásadní roli v mnoho matematických pojmů a teorie, jako je Pythagorova věta, Diofantova aproximace a pokračující zlomky.
Rozdíl mezi racionálními a iracionálními čísly
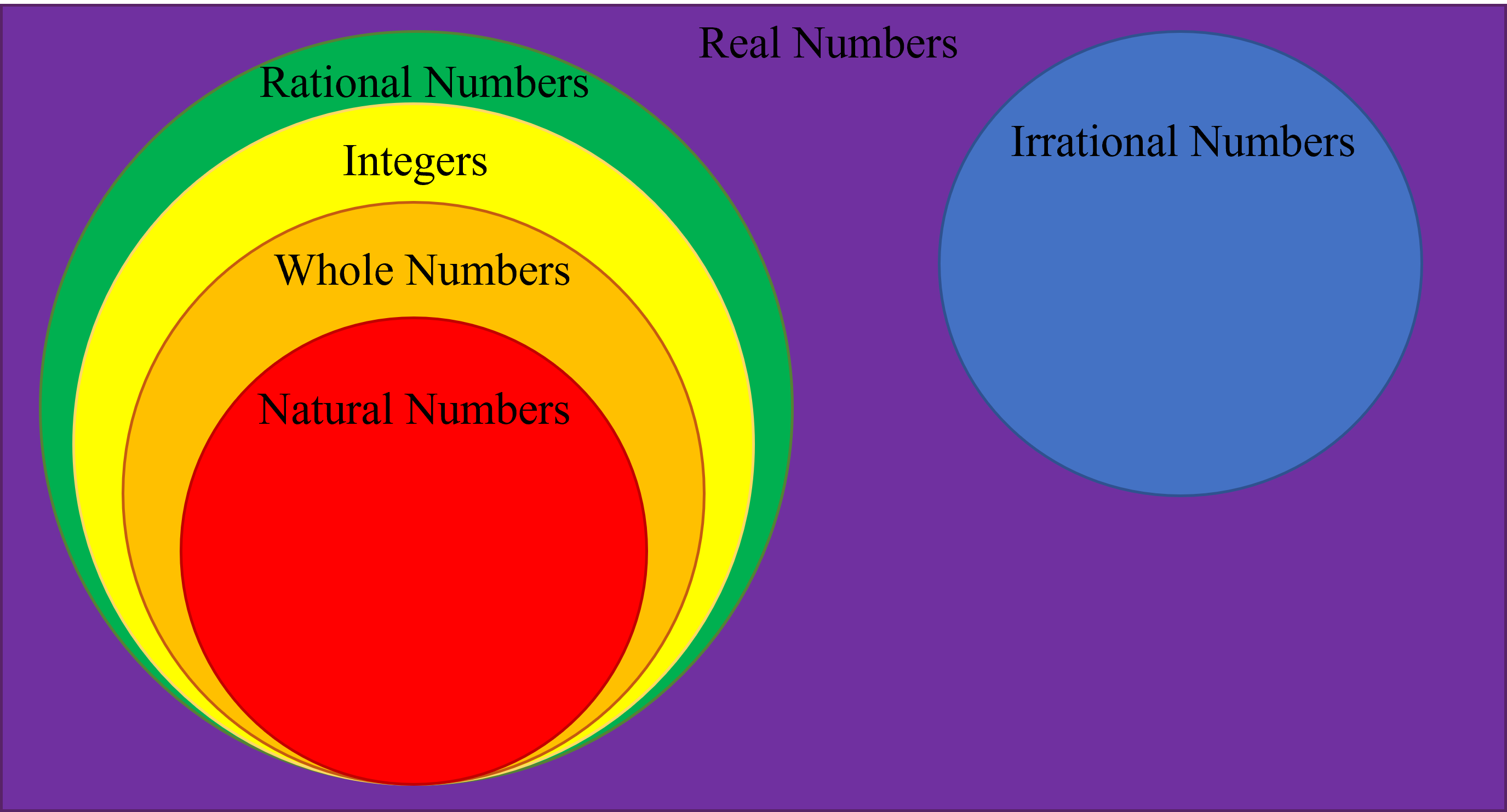
Definice racionálních čísel
V říši reálné číslos, existuje zásadní rozdíl mezi racionálními a iracionálními čísly. Racionální čísla lze definovat jako jakékoli číslo, které lze vyjádřit jako zlomek, kde jak čitatel a jmenovatel jsou celá čísla. Tato čísla mohou být reprezentována jako non-opakující se a neukončující desetinná místa. Například 1/2, 3/4 a -5/7 jsou všechna racionální čísla.
Jak se iracionální čísla liší od racionálních čísel
On druhá ruka, iracionální čísla jsou ta, která nelze vyjádřit zlomkem. Mají nekonečno desetinné rozšíření která se neopakuje ani nekončí. Některé známé příklady mezi iracionální čísla patří náměstí odmocnina ze 2 (√2), matematická konstanta Pi (π) a transcendentální číslo e (Eulerovo číslo). Tato čísla mají jedinečné vlastnosti, které je odlišují od racionálních čísel.
Racionální vs iracionální čísla: Srovnávací analýza
Pro lepší pochopení rozdíl mezi racionálními a iracionálními čísly, srovnejme jejich vlastnosti:
| Vlastnictví | Racionální čísla | Iracionální čísla |
|---|---|---|
| Reprezentace | Lze vyjádřit zlomkem | Nelze vyjádřit zlomkem |
| Desetinná expanze | Neopakující se a neukončující | Nekonečné a neopakující se |
| Příklady | 1/2, 3/4, -5/7 | √2, π, e |
| Výskyt | Počitatelné a diskrétní | Nespočetné a nepřetržité |
| Velikost | Lze porovnávat pomocí poměrů | Nelze porovnávat pomocí poměrů |
| Důkaz iracionality | Lze dokázat pomocí algebraických metod | Často se ukázalo pomocí matematických důkazů iracionality, jako je Cantorův důkaz |
Rozdíl mezi racionálními a iracionálními čísly téma od té doby zajímavé prastaré časy. Ve skutečnosti, starověcí řečtí matematici, jako je Euclid v jeho „Prvky“ a Eudoxus s jeho teorie proporcí, prozkoumal koncept iracionálních čísel. Tito raní matematici objevil to určité veličiny, jako náměstí odmocnina ze 2, nelze vyjádřit jako poměr celých čísel.
Koncept problémů s iracionálními čísly naše konvenční chápání čísel a jejich velikosti. To dokazuje ne všechna množství lze úhledně reprezentovat celými čísly nebo poměry. Existence iracionálních čísel, s jejich nekonečný desetinné rozšířenís, prozrazuje bohatství a složitost matematická teorie.
Povaha iracionálních čísel
Jsou iracionální čísla skutečná?
Iracionální čísla jsou v matematice fascinujícím pojmem. Oni jsou reálné číslos, které nelze vyjádřit jako jednoduchý zlomek nebo podíl dvou celých čísel. Na rozdíl od racionálních čísel, která lze zapsat jako koncová nebo opakující se desetinná místa, mají iracionální čísla neopakující se a neukončující desetinné rozšířenís. To znamená, že jejich desítkové zastoupení pokračuje navždy bez jakéhokoli vzoru.
Jeden slavný příklad iracionálního čísla je náměstí odmocnina ze 2 (√2). Když je vyjádřen jako desetinné číslo, pokračuje donekonečna bez opakování. Další známé iracionální číslo je Pi (π), které představuje poměr obvodu kruhu k jeho průměru. Pi je také neopakující se a neukončující desetinné místo.
Mohou být iracionální čísla záporná?
Ano, iracionální čísla mohou být záporná. Negativnost nebo pozitivita číslo je nezávislý na jeho racionalita nebo iracionalita. Zda číslo je racionální nebo iracionální, je určeno výhradně tím jeho schopnost být vyjádřen jako zlomek nebo podíl dvou celých čísel. Takže, stejně jako racionální čísla, iracionální čísla mohou být kladná nebo záporná.
Například, náměstí odmocnina 2 (√2) je iracionální číslo a může být kladné i záporné. Podobně Pi (π) je také iracionální číslo, které může být kladné nebo záporné, v závislosti na kontext ve kterém se používá.
Jsou iracionální čísla nekonečná?
Ano, iracionální čísla mají nekonečno desetinné rozšíření. Na rozdíl od racionálních čísel, která mohou mít buď ukončení nebo opakování desítkové zastoupení, iracionální čísla mají desetinné rozšířeníkteré pokračují navždy bez opakování. Tato nekonečná příroda Jejich desítkové zastoupení je jeden z definující vlastnosti iracionálních čísel.
Například, náměstí odmocnina ze 2 (√2) má nekonečno desetinné rozšíření která se nikdy neopakuje. Totéž platí pro další iracionální čísla jako Pi (π) a zlatý řez. Tato nekonečná příroda Jejich desetinné rozšířenís činí iracionální čísla zajímavými a náročnými na práci matematické výpočty.
Jsou iracionální čísla neukončující?
Ano, iracionální čísla mají neukončení desetinné rozšířenís. To znamená, že jejich desítkové zastoupení nepřijde konec nebo ukončit po konečný počet číslic. Namísto, číslice pokračovat donekonečna bez jakýkoli opakující se vzor.
Například, náměstí odmocnina z 2 (√2) má neukončovací desetinné rozšíření to pokračuje donekonečna bez opakování. Podobně Pi (π) a další iracionální čísla mají také neukončující desetinné rozšířenís. Tato vlastnost rozlišuje iracionální čísla od racionálních čísel, která mohou mít zakončení desítkové zastoupenís.
Význam iracionálních čísel
Iracionální čísla hrají v matematice zásadní roli, poskytují hlubší porozumění of příroda čísel a jejich vztahy. Jsou fascinujícím konceptem, který je výzvou naše konvenční chápání čísel jako racionálních nebo celých. Pojďme prozkoumat význam iracionálních čísel a proč jsou v matematice tak důležitá.
Proč byla vynalezena iracionální čísla?
Vynález iracionálních čísel byl řízen potřeba reprezentovat množství, která nemohla být vyjádřena jako zlomky nebo poměry celých čísel. Staří Řekové, zejména Pythagorejci, to zjistil určité délky, Jako úhlopříčka of čtverec se stranami délky 1 nelze vyjádřit jako racionální číslo. Toto uvědomění vedl k vývoj iracionálních čísel jako způsob zastupovat tyto ne-opakující se a neukončující desetinná místa.
Proč existují iracionální čísla?
Iracionální čísla existují, protože existují matematické veličiny které nelze přesně reprezentovat racionálními čísly. Nejznámější příklad is náměstí odmocnina ze 2, kterou nelze vyjádřit zlomkem. Tato nekonečná desetinné rozšíření of √2 je neopakující se a neukončující číslo, což z něj činí iracionální číslo. Podobně, jiné matematické konstanty jako Pi a Eulerovo číslo e) jsou rovněž iracionální, s nekonečný desetinné rozšířenís které se neopakují ani neukončují.
Význam iracionálních čísel v matematice
Iracionální čísla mají několik důležitých aplikací v matematice. Jsou základní v geometrii, zejména v důkaz Pythagorovy věty. Pythagorova věta říká, že v pravoúhlém trojúhelníku náměstí přepony se rovná součet of náměstíů další dvě strany. Důkaz of tato věta zahrnuje použití iracionálních čísel, as délkas zúčastněných stran jsou často iracionální.
Další významná aplikace iracionálních čísel je v konceptu zlatý řez. Tento poměr, označeno řecké písmeno φ (phi), je iracionální číslo, které bylo uctíváno jeho estetické vlastnosti. Objeví se v různé přírodní a umělecké jevy, Jako proporce of Parthenon v Aténách a vzorce růstu of určité rostliny.
Kromě toho jsou iracionální čísla nezbytná pole of teorie čísel, kde pomáhají zakládat vlastnosti a vztahy mezi odlišné typy čísel. Hrají také zásadní roli studie kalkulu, kde se používají k definování a analýze spojité funkce.
Zkoumání konkrétních iracionálních čísel
Pi jako iracionální číslo
Pi, značeno řecké písmeno π, je fascinující a dobře známé iracionální číslo. Je definován jako poměr obvodu kruhu k jeho průměru. Pi je a reálné číslo a neopakující se desetinné místo bez konce. Jeho desítkové zastoupení jde donekonečna bez vzor. Hodnota pí je přibližně 3.14159, ale bylo vypočítáno na miliardy desetinná místa.
Piho iracionalita bylo prokázáno tím Johann Lambert v roce 1768 a bylo předmět fascinace pro matematiky v celé historii. Důkaz jeho iracionality zahrnuje použití Pythagorovy věty a konceptu hranaté kořeny. Pi je také transcendentální číslo, což znamená, že není algebraické číslo a nelze je vyjádřit jako kořen of jakákoli polynomická rovnice s celočíselné koeficienty.
Iracionální číslo "e"
Další důležité iracionální číslo je 'e', také známé jako Eulerovo číslo. 'e' je matematická konstanta což se přibližně rovná 2.71828. Stejně jako pí je 'e' neopakující se desetinné místo bez konce. Je to také transcendentální číslo.
Hodnota z 'e' přirozeně vzniká v různé matematické souvislosti, jako je složený úrok, exponenciální růst a počet. Poprvé ji představil švýcarský matematik Leonhard Euler in 18. století. 'e' má četné aplikace v oborech jako fyzika, inženýrství a finance.
Iracionální číslo mezi 4 a 5
Mezi celá čísla 4 a 5 leží iracionální číslo. Tohle číslo is neracionální číslo, což znamená, že jej nelze vyjádřit jako zlomek dvou celých čísel. Má nekonečno desetinné rozšíření bez jakýkoli opakující se vzor. Toto iracionální číslo spadá do oblasti matematická iracionalita, která se zabývá čísly, která nelze reprezentovat jako podíly celých čísel.
Přesná hodnota of toto iracionální číslo mezi 4 a 5 není známo, ale lze jej aproximovat pomocí různý matematické techniky, jako je diofantická aproximace a pokračovací zlomky. Tyto metody dovolte nám být blíž a blíž skutečnou hodnotu of číslo pomocí racionální aproximace.
Iracionální číslo mezi 2 a 2.5
Podobně mezi číslos 2 a 2.5 existuje další iracionální číslo. Tohle číslo, stejně jako předchozí, nelze vyjádřit jako zlomek a má nekonečno desetinné rozšíření. Spadá do kategorii of neracionální čísla, což jsou podmnožina iracionálních čísel.
Přesná hodnota of toto iracionální číslo mezi 2 a 2.5 je také neznámá, ale lze ji aproximovat pomocí matematické techniky jako jsou pokračující zlomky a koncept Dedekind škrty. Tyto metody dovolte nám najít racionální aproximace které se postupně přibližují skutečnou hodnotu of číslo.
Praktické aplikace iracionálních čísel
Iracionální čísla jsou fascinujícím pojmem v matematice, která má četné praktické aplikace in různých polí. Tato čísla, která nelze vyjádřit jako zlomek nebo podíl dvou celých čísel, hrají zásadní roli mnoho reálných scénářů. Pojďme prozkoumat některé praktické aplikace iracionálních čísel.
Jak najít iracionální číslo
Najít iracionální číslo může být zajímavý úkol. Jeden společný způsob identifikovat iracionální číslo je hledáním neopakujícího se a neukončujícího čísla desetinné rozšířenís. Například, náměstí odmocnina 2 (√2) je iracionální číslo. Když je vyjádřen jako desetinné číslo, pokračuje donekonečna bez opakování jakéhokoli vzoru. Podobně, matematická konstanta Pi (π) je další známé iracionální číslo což představuje poměr obvodu kruhu k jeho průměru.
Jak převést iracionální číslo na zlomek
Převod iracionálního čísla na zlomek je náročný úkol protože iracionální čísla z definice nelze vyjádřit jako poměr dvou celých čísel. Nicméně existují aproximační metody jako pokračující zlomky a diofantická aproximace, které mohou poskytnout aproximace racionálních čísel pro iracionální čísla. Tyto aproximace může být užitečné v praktických aplikacích, kde je práce s racionálními čísly pohodlnější.
Cvičební problémy zahrnující iracionální čísla
Práce s iracionálními čísly se neomezuje pouze na teoretické koncepty ale nachází uplatnění i při řešení problémy reálného světa. Pojďme vzít pohled at nějaké praktické problémy zahrnující iracionální čísla:
Pythagorova věta: Pythagorova věta, která spojuje strany pravoúhlého trojúhelníku, často zahrnuje použití iracionálních čísel. Například při nálezu délka přepony v pravoúhlý trojúhelník se stranami délky 1, náměstí odmocnina 2 (√2) se jeví jako iracionální číslo.
Zlatý poměr: Zlatý řez, označený řecké písmeno phi (φ), je iracionální číslo, které se po staletí používá v umění, architektuře a designu. Reprezentuje vizuálně příjemný poměr a lze je nalézt v různé přírodní a člověkem vytvořené stavby.
Eulerovo číslo: Eulerovo číslo (e) je další důležité iracionální číslo, které se objevuje v různé matematické a vědecké aplikace, Jako výpočty složeného úroku, modely exponenciálního růstu, a analýza komplexních čísel.
Jaký je vztah mezi iracionálními čísly a sousedními úhly?
Pochopení konceptů a vlastností sousedních úhlů. Abychom prozkoumali průsečík s iracionálními čísly, můžeme zvážit měření úhlů v kruhu. Při určování velikosti úhlu ve stupních je zásadní pracovat s racionálními čísly. Při použití radiánů, které úzce souvisejí s kružnicemi a trigonometrií, však mohou úhly zahrnovat iracionální čísla. Například úhel měřící 180 stupňů je ekvivalentní π radiánům, kde π je iracionální číslo. Toto spojení mezi sousedními úhly a iracionálními čísly zdůrazňuje jejich význam při studiu kružnic a goniometrických funkcí, jak je vysvětleno v Pochopení konceptů a vlastností sousedních úhlů.
Často kladené otázky
1. Co je to iracionální číslo v matematice?
Iracionální číslo v matematice je libovolné reálné číslo které nelze vyjádřit jako poměr dvou celých čísel. Tato čísla mají neukončující a neopakující se desetinné rozšířenís. Příklady zahrnují náměstí kořen libovolného čísla, které není dokonalý čtverec, Pi a Eulerovo číslo.
2. Jaké jsou příklady iracionálních čísel?
Příklady iracionálních čísel zahrnují Pi (přibližně 3.14159), Eulerovo číslo (přibližně 2.71828), náměstí kořen 2 a zlatý řez (přibližně 1.61803). Tato čísla jsou iracionální, protože jejich desetinné rozšířenís jsou neukončující a neopakující se.
3. Jak se liší iracionální číslo od racionálního čísla?
Racionální čísla lze vyjádřit jako poměr dvou celých čísel, zatímco iracionální čísla nikoli. v jiná slova, racionální číslo lze zapsat jako zlomek, zatímco iracionální číslo nikoli. Kromě toho, desetinné rozšíření racionálního čísla buď končí nebo se opakuje, zatímco desetinné rozšíření iracionálního čísla nedělá ani jedno.
4. Je iracionální číslo reálné číslo?
Ano, iracionální číslo je a reálné číslo, reálné číslopatří obě racionální čísla a iracionální čísla. To znamená, že jakékoli číslo, které lze nalézt na číslo linka je a reálné číslovčetně iracionálních čísel.
5. Proč jsou iracionální čísla nekonečná?
Iracionální čísla jsou nekonečná, protože jejich desetinné rozšířenís jsou neukončující. To znamená, že desítkové zastoupení iracionálního čísla pokračuje navždy bez opakování. Tohle je výsledek of skutečnost že iracionální čísla nelze vyjádřit jako podíl dvou celých čísel.
6. Jaký je symbol pro iracionální číslo?
Není tam všeobecně uznávaný symbol pro iracionální čísla. Často jsou však zastoupeni soubor of reálné číslos (označené R) s výjimkou soubor racionálních čísel (označené Q).
7. Jak byla objevena iracionální čísla?
Koncept iracionálních čísel lze zpětně vysledovat starověká řecká matematika, konkrétně v Euklidovy prvky. Objev že náměstí odmocnina 2 je iracionální je připsána Pythagorejci, skupina matematiků v Starověké Řecko.
8. Jak identifikovat iracionální číslo?
Iracionální číslo lze identifikovat, pokud je desetinné rozšíření je neukončující a neopakující se. Navíc iracionální číslo nelze vyjádřit jako zlomek nebo podíl dvou celých čísel.
9. Může být součin dvou iracionálních čísel racionální?
Ano, produkt of dvě iracionální čísla může být racionální. Například, náměstí odmocnina ze 2 je iracionální číslo. Pokud se množíte náměstí kořen 2 sám o sobě, výsledek je 2, což je racionální číslo.
10. Proč jsou v matematice důležitá iracionální čísla?
Iracionální čísla jsou v matematice důležitá, protože se vyplňují mezery” mezi racionálními čísly na číslo linka, která to zajistí libovolnou délku lze měřit. Vznikají také přirozeně v mnoho oblastí matematiky, včetně geometrie, počtu a teorie čísel.
Také čtení:
- Fluorescenční mikroskopie
- Chromatin vs chromatid
- Je nezávislá sortimentní mutace
- Oblast kruhu
- Axiomy
- Termosféra 2
- Element 115
- Co je směrový indikátor směrové gyro
- Adsorpce vs absorpce
- servopohony

Základní tým TechieScience pro malé a střední podniky je skupina zkušených odborníků z různých vědeckých a technických oborů včetně fyziky, chemie, technologie, elektroniky a elektrotechniky, automobilového průmyslu a strojního inženýrství. Náš tým spolupracuje na vytváření vysoce kvalitních, dobře prozkoumaných článků o široké škále vědeckých a technologických témat pro web TechieScience.com.
Všechny naše senior SME mají více než 7 let zkušeností v příslušných oborech. Jsou to buď profesionálové z pracovního průmyslu, nebo jsou spojeni s různými univerzitami. Odkazovat Naši autoři Stránka, kde se dozvíte o našich základních malých a středních podnicích.

Ahoj kolego čtenáři,
Jsme malý tým v Techiescience, tvrdě pracujeme mezi velkými hráči. Pokud se vám líbí, co vidíte, sdílejte náš obsah na sociálních sítích. Vaše podpora znamená velký rozdíl. Děkuji!